Description

Farmer John's farm has many pastures. Some paths connect specific pairs of pastures. A set of interconnected pastures is called a pasture group. However, as of now, you can see that there are at least two pasture groups that are not connected. Now, John wants to add exactly one path to the farm with the following constraint: The diameter of a pasture group is defined as the distance between the two farthest pastures in the group (all distances mentioned in this problem refer to the shortest path distances). Consider the following two pasture groups, as shown in Figure 1, which has five pastures marked with "*" and paths represented by straight lines. Each pasture has its own coordinates: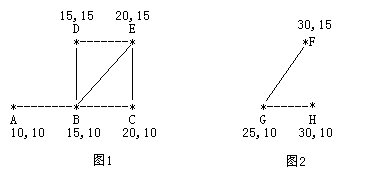
The diameter of the pasture group in Figure 1 is approximately 12.07106, with the farthest pastures being A and E, and the shortest path between them being A-B-E. Both of these pasture groups are located on John's farm. John will select one pasture from each group and connect them with a path such that the resulting larger pasture group has the smallest possible diameter. Note that if two paths intersect midway, we do not consider them connected. Only if two paths intersect at a common pasture do we consider them connected. Your task is to write a program to find such a path connecting two different pasture groups, ensuring that the new larger pasture group formed has the smallest possible diameter.

Input Format

• Line 1: An integer N (1 ≤ N ≤ 150), representing the number of pastures.
• Lines 2 to N+1: Each line contains two integers X and Y (0 ≤ X, Y ≤ 100000), representing the coordinates of the N pastures. Each pasture's coordinates are unique.
• Lines N+2 to 2*N+1: Each line contains N numbers (0 or 1) representing a symmetric adjacency matrix. For example, the matrix for the two pasture groups described in the problem is as follows:

  A B C D E F G H 
  A 0 1 0 0 0 0 0 0 
  B 1 0 1 1 1 0 0 0 
  C 0 1 0 0 1 0 0 0 
  D 0 1 0 0 1 0 0 0 
  E 0 1 1 1 0 0 0 0 
  F 0 0 0 0 0 0 1 0 
  G 0 0 0 0 0 1 0 1 
  H 0 0 0 0 0 0 1 0 
  

Output Format

A single line containing a real number, representing the desired answer, rounded to six decimal places.

A B C D E F G H 
A 0 1 0 0 0 0 0 0 
B 1 0 1 1 1 0 0 0 
C 0 1 0 0 1 0 0 0 
D 0 1 0 0 1 0 0 0 
E 0 1 1 1 0 0 0 0 
F 0 0 0 0 0 0 1 0 
G 0 0 0 0 0 1 0 1 
H 0 0 0 0 0 0 1 0

8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010