#Q85. 「一本通 3.3 例 2」双调路径
「一本通 3.3 例 2」双调路径
Description
Original Source: BalticOI 2002
Road toll systems are rapidly evolving. With the increasing density of roads, choosing the optimal path has become a practical concern. The roads in the city are bidirectional, and each road has a fixed travel time and a cost associated with it.
A path consists of a sequence of connected roads. The total time is the sum of the travel times of the individual roads, and the total cost is the sum of the costs of the roads traversed. A path is considered better if it is either faster or cheaper than another path. More precisely, if a path is strictly faster and not more expensive, it is better. The converse also holds true. If no other path is better than a given path, that path is called a minimal path.
There may be multiple such minimal paths or none at all.
Problem: Read the network and compute the total number of distinct minimal paths. Two minimal paths with identical cost and time are considered the same. You only need to output the count of distinct minimal paths.
Input Format
The first line contains four integers: the total number of cities , the total number of roads , the starting city , and the destination city ;
The next lines each describe a road with four integers: the two endpoints and , the cost , and the time ;
There may be multiple roads connecting the same pair of cities.
Output Format
A single integer representing the total number of distinct minimal paths.
Sample 1
Sample input as shown below:
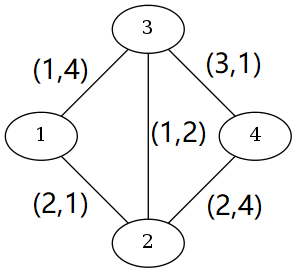
There are 4 paths from to . They are (cost , time ), (cost , time ), (cost , time ), and (cost , time ).
and are better than . There are two optimal paths: one with cost and time ( and ) and another with cost and time ().
4 5 1 4
2 1 2 1
3 4 3 1
2 3 1 2
3 1 1 4
2 4 2 4
2
Data Range and Hints
For all data, $1\le n\le 100,0\le m\le 300,1\le s,e,p,r\le n,0\le c,t\le 100$. It is guaranteed that and .
