Description

Original Problem from: ICPC Tehran 1999

CE Digital Company has developed a product called the Automatic Painting Machine (APM). It can paint a flat panel composed of non-overlapping rectangles of different sizes with predetermined colors.

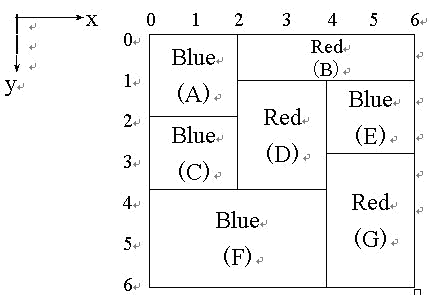
To perform the painting, APM requires a set of brushes. Each brush is dipped in a color $C$. The APM picks up a brush dipped in color $C$ and paints all rectangles that are colored $C$. Note that there is an order requirement for painting: to prevent color mixing due to pigment leakage, a rectangle can only be painted after all rectangles immediately above it have been painted. For example, in the figure, rectangle $F$ must be painted after $C$ and $D$ have been painted. Note that each rectangle must be fully painted at once; partial painting is not allowed.

Write a program to find a painting sequence that minimizes the number of times the APM picks up a brush. Note that if a brush is picked up more than once, each instance must be counted in the total.

Input Format

The first line contains the number of rectangles $N$.
The following $N$ lines describe the $N$ rectangles. Each rectangle is described by 5 integers: the $y$ and $x$ coordinates of the top-left corner, the $y$ and $x$ coordinates of the bottom-right corner, and the predetermined color.

Output Format

A single integer representing the minimum number of times the brushes are picked up.

Sample 1

7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

3

Constraints & Hints

For all data, $1 \leq N \leq 14$, and the color codes are integers from $1$ to $20$. It is guaranteed that the top-left corner of the panel is always $(0, 0)$, and the coordinate range is from $0$ to $9$.