#Q134. 「一本通 4.4 例 3」异象石
「一本通 4.4 例 3」异象石
Description
Original Source: Contest Hunter Round #56
In the alternate dimension of Adera, there is a map. This map contains points connected by bidirectional edges. Initially, there are no anomaly stones on the map. Over the next moments, one of the following three types of events will occur at each moment:
- An anomaly stone appears at a certain point on the map (points that already have an anomaly stone will not reappear);
- An anomaly stone at a certain point on the map is destroyed (points without anomaly stones will not be destroyed);
- The player is asked to determine the minimum total length of the edge set required to connect all points currently containing anomaly stones.
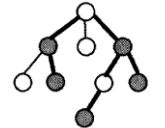
As the player, please answer these queries. The figure below is an example, where gray nodes represent points with anomaly stones, and bold edges indicate the selected edge set for connecting the anomaly stones.
Input Format
The first line contains an integer , indicating the number of points;
The next lines each contain three integers , indicating a bidirectional edge between point and with length ;
The -th line contains a positive integer ;
The following lines each describe an event, which is one of the following three formats:
+ x: Indicates that an anomaly stone appears at point ;- x: Indicates that the anomaly stone at point is destroyed;?: Asks for the minimum total length of the edge set required to connect all points currently containing anomaly stones.
Output Format
For each ? event, output an integer representing the answer.
Sample 1
6
1 2 1
1 3 5
4 1 7
4 5 3
6 4 2
10
+ 3
+ 1
?
+ 6
?
+ 5
?
- 6
- 3
?
5
14
17
10
Data Range and Hints
For of the data, ;
For another of the data, the map is either a chain or a star-shaped graph;
For of the data, $1\le n, m \le 10^5, 1 \le x, y \le n, x \not = y, 1 \le z \le 10^9$.
