Description

Original source: POI 2008 Stage 2

Byteotia has $n$ towns. Some towns are connected by bidirectional roads. Although there may be bridges, tunnels, or overpasses, there are no intersections outside the towns. Each pair of towns is connected by at most one road. A person can travel from any town to any other town—directly or indirectly.

Each town has exactly one resident. Therefore, the residents are quite lonely. In fact, each resident wants to visit every other resident (at the other resident's location) exactly once. Thus, exactly $n\cdot (n-1)$ visits should take place. Unfortunately, a general strike by programmers, who demand immediate payment for their developed programs, is ongoing. As a protest measure, the programmers plan to blockade one town in Byteotia, preventing anyone from entering, leaving, or passing through that town. As we speak, they are debating which town to choose to cause the most severe consequences.

Write a program that reads Byteotia's road network from standard input and outputs, for each specified town, how many visits cannot be made if the programmers blockade that town?

Brief Description

Byteotia has $n$ towns and $m$ bidirectional roads. Each road connects two different towns, with no duplicate roads, and all towns are connected.
Output $n$ numbers, representing how many ordered pairs of towns cannot reach each other if all edges connected to the $i$-th town are removed.

Input Format

Input $n,m$ and $m$ edges.

Output Format

Output $n$ numbers, representing how many ordered pairs of towns cannot reach each other if all edges connected to the $i$-th town are removed.

Sample 1

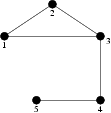
5 5
1 2
2 3
1 3
3 4
4 5

8
8
16
14
8

Data Range and Hint

$n\le 10^5, m\le 5\times 10^5$.