Description

Original source: USACO 2006 Jan. Gold

To move from one of the $F$ pastures to another, Bessie and her companions have to pass through some terrifying trees they dislike. The cows are tired of being forced to take a certain path, so they want to build some new roads such that there are at least two mutually separated paths between every pair of pastures, giving them more choices.

There is already at least one path between every pair of pastures. Given the descriptions of all $R$ bidirectional roads, where each road connects two distinct pastures, calculate the minimum number of new roads that need to be built.

A path is formed by connecting several roads end-to-end. Two paths are mutually separated if they share no common roads, although they may pass through some of the same pastures.

For the same pair of pastures, there might already be two different roads. You can also build another road between them as a distinct additional road.

Input Format

The first line contains two integers $F$ and $R$;

The next $R$ lines each contain two integers representing two pastures connected by a road.

Output Format

Output the minimum number of new roads that need to be built.

Sample 1

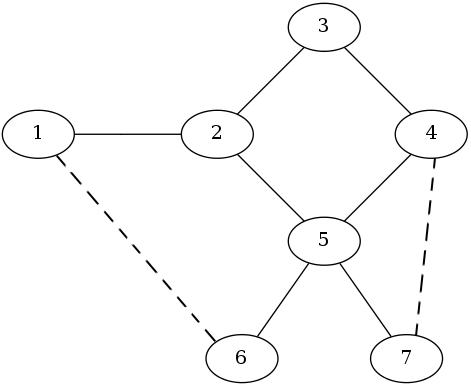
The solid lines in the figure represent existing roads, while the dashed lines represent the two newly built roads. Now, some paths can be verified, for example:

Pasture $1$ and pasture $2$: $1→2$ and $1→6→5→2$

Pasture $1$ and pasture $4$: $1→2→3→4$ and $1→6→5→4$

Pasture $3$ and pasture $7$: $3→4→7$ and $3→2→5→7$

In fact, every pair of pastures is connected by two separated paths.

7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7

2

Constraints & Hints

$1 \le F \le 5000,F-1 \le R \le 10000$.