Description

Original source: BZOJ 3907

The streets of a certain city form a grid, with the bottom-left corner at coordinate $A(0, 0)$ and the top-right corner at coordinate $B(n, m)$, where $n \ge m$. Starting from point $A(0, 0)$, you can only move along the streets to the right or upwards. Additionally, you cannot pass through any point above the diagonal line shown in the figure, meaning any point $(x, y)$ on the path must satisfy $x \ge y$. Under these constraints, how many distinct paths are there to reach $B(n, m)$?

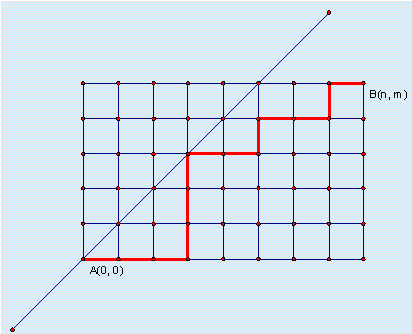
Input Format

The input consists of a single line containing two integers $n$ and $m$, representing the dimensions of the city grid.

Output Format

Output a single integer followed by a line break or carriage return, indicating the total number of distinct paths.

Sample 1

6 6

132

Constraints & Notes

For all test cases, $1\le m\le n\le 5000$.