Description

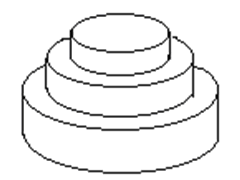
Mr. W wants to make an M-layer birthday cake with a volume of $N\pi$, where each layer is a cylinder.

Let the i-th layer of the cake from the bottom up be a cylinder with radius $R_i$ and height $H_i$. For $i < M$, it is required that $R_i > R_{i+1}$ and $H_i > H_{i+1}$. Since we need to apply cream to the cake, we want to minimize the surface area $Q$ of the cake (excluding the bottom surface of the lowest layer).

Let $Q = S\pi$. For given $N$ and $M$, write a program to find the cake's design (appropriate values of $R_i$ and $H_i$) that minimizes $S$. (All data above, except for $Q$, are positive integers.)

Input Format

The first line contains $N$, indicating the cake's volume is $N\pi$.

The second line contains $M$, indicating the number of layers in the cake.

Output Format

Output a single line with an integer $S$ (if no solution exists, output $S=0$).

Sample 1

Note: Cylinder formulas: Volume $V=\pi R^2H$; Lateral surface area $S’=2\pi RH$; Base area $S=\pi R^2$.

100
2

68

Data Range and Hints

For all data, $1 \leq N \leq 10^4$, $1 \leq M \leq 20$.