Description

Original source: CEOI 2004

From the top of the mountain to the bottom along a straight line, there are $n$ old trees planted. The local government has decided to cut them down. To avoid wasting any timber, the trees must be transported to sawmills after being felled.
The timber can only be transported downhill. There is a sawmill at the foot of the mountain. Two additional sawmills will be newly built along the mountain path. You must decide where to build these two sawmills to minimize the total transportation cost. It is assumed that transporting one kilogram of timber per meter costs one cent.
Your task is to write a program that reads the number of trees, their weights, and positions, and calculates the minimum transportation cost.

Input Format

The first line of input is a positive integer $n$, representing the number of trees. The trees are labeled from $1$ to $n$ from the mountain top to the foot.
The next $n$ lines each contain two integers $w_i$ and $d_i$. These represent the weight (in kilograms) of the $i$-th tree and the distance between the $i$-th tree and the $(i+1)$-th tree, respectively. The last number $d_n$ represents the distance from the $n$-th tree to the sawmill at the foot of the mountain.

Output Format

Output only one number, representing the minimum transportation cost.

Sample 1

The figure below illustrates the optimal sawmill locations for the sample input. Trees are represented by circles, and sawmills are marked in black. The result is:

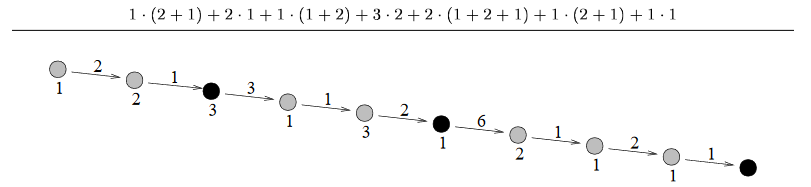
9
1 2
2 1
3 3
1 1
3 2
1 6
2 1
1 2
1 1

26

Data Range and Hints

For $97$ points of the data, $2\le n\le 2\times 10^4, 1\le w_i\le 10^4, 0\le d_i\le 10^4$. It is guaranteed that the cost to transport all trees to the sawmill at the foot of the mountain is less than $2\times 10^9$ cents. (This part of the data is the original dataset.)

For the remaining $3$ points of the data, $2\le n\le 2\times 10^5$, and all calculations can be performed within 64-bit signed integers.