Description

Original source: ZJOI 2007

L Company has several factories on a mountain. Due to the mountain's location in an inland plateau area (dry with little rain), L Company usually stores its products directly outdoors to save costs. Suddenly one day, Mr. L, the president of L Company, received a call from the meteorological department informing him that a heavy rainstorm would arrive in three days. Thus, Mr. L decided to urgently build warehouses in some factories to prevent the products from being damaged by the rain.

L Company has $N$ factories on the mountain. As shown in the figure, Factory $1$ is at the mountaintop, and Factory $N$ is at the mountain base.

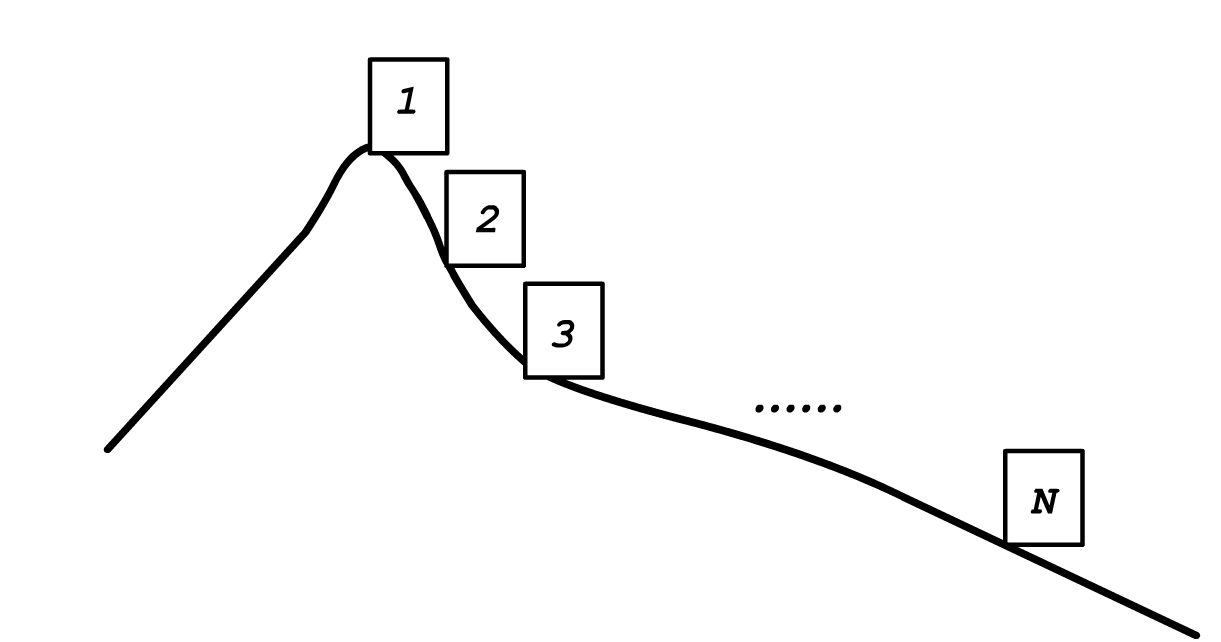
Due to the varying terrain, the cost of building a warehouse may differ across factories. Factory $i$ currently has $P_i$ finished products, and the cost of building a warehouse in this factory is $C_i$. For factories without a warehouse, their products must be transported to other warehouses for storage. Since L Company's product sales office is located at Factory $N$ at the mountain base, products can only be transported downhill (i.e., only to warehouses of factories with larger indices). Of course, transporting products also incurs costs—the cost of moving one product one unit distance is $1$. It is assumed that the capacity of all warehouses is sufficiently large to accommodate all products.

The following are known:

1. The distance of Factory $i$ from Factory $1$, denoted as $X_i$ (where $X_1=0$);
2. The current number of finished products in Factory $i$, denoted as $P_i$;
3. The cost of building a warehouse in Factory $i$, denoted as $C_i$.

Please help L Company find a warehouse construction plan that minimizes the total cost (construction cost + transportation cost).

Input Format

The first line contains an integer $N$, the number of factories. Next, $N$ lines follow, each containing three integers $X_i,$ $P_i,$ and $C_i$, as described in the problem statement.

Output Format

Output a single integer, the minimum total cost achievable with the optimal plan.

Sample 1

Building warehouses in Factory $1$ and Factory $3$ incurs a construction cost of $10+10=20$ and a transportation cost of $(9-5)\times 3 = 12$, resulting in a total cost of $32$. If a warehouse is built only in Factory $3$, the construction cost is $10$, and the transportation cost is $(9-0)\times 5$ $+(9-5)\times 3$ $=57$, resulting in a total cost of $67$, which is worse than the first plan.

3
0 5 10
5 3 100
9 6 10

32

Data Range and Hints

For all data, $N \le 10^6$. It is guaranteed that all $X_i,$ $P_i,$ and $C_i$ are within the int range, and intermediate calculation results will not exceed the long long range.