Description

A point spreads one unit distance in four directions every unit of time, as shown in the figure: two points $a$ and $b$ are considered connected, denoted as $e(a,b)$, if and only if their spreading regions have a common area. The definition of a connected block is that for any two points $u$ and $v$ within the block, there must exist a path $e(u,a_0), e(a_0,a_1),…, e(a_k,v)$.

Given $n$ points on a plane, determine the earliest time at which they form a connected block.

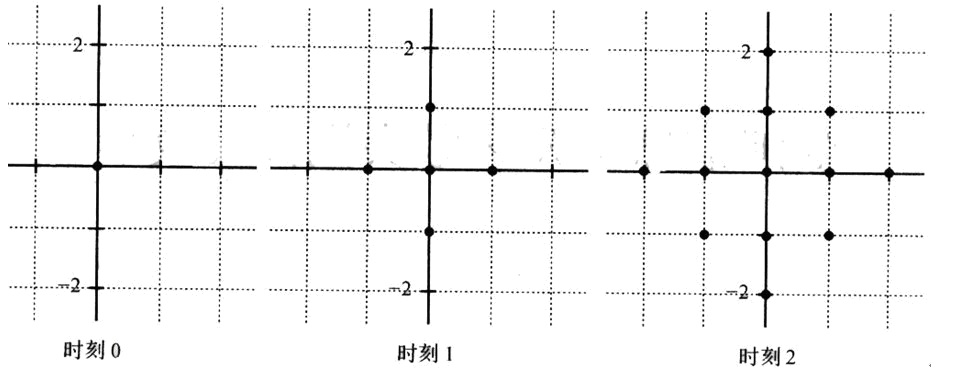
Input Format

The first line contains an integer $n$, followed by $n$ lines, each containing the coordinates of a point.

Output Format

Output a single integer representing the earliest time at which all points form a connected block.

Sample 1

2
0 0
5 5

5

Data Range and Hints

For $20\%$ of the data, it is guaranteed that $1 \leq n \leq 5, 1 \leq X_i, Y_i \leq 50$;

For $100\%$ of the data, it is guaranteed that $1 \leq n \leq 50, 1 \leq X_i, Y_i \leq 10^9$.